[정렬] Radix Sort(기수 정렬) 정리
2022. 10. 19. 17:10ㆍTIL💡/Algorithms
How Radix Sort works?
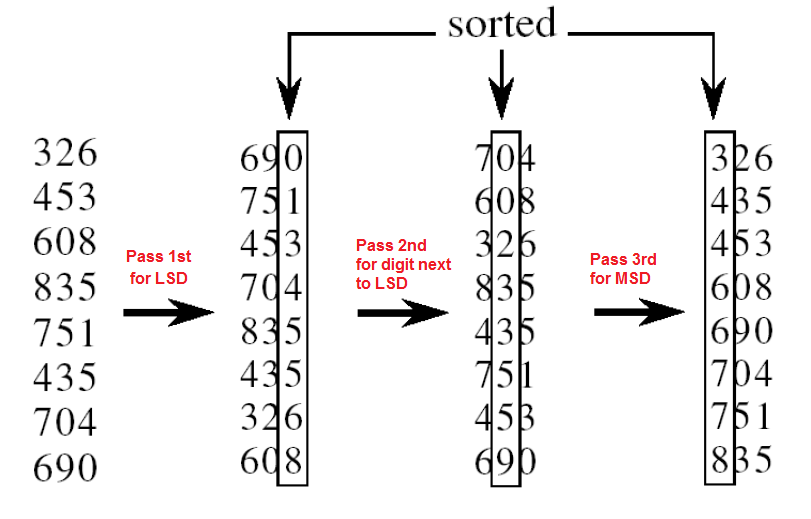
구성요소들을 마지막 자릿수 기반으로 정렬한다.(Least Significant Digit)
그리고 그 결과는 다시 마지막에서 두 번째 자릿수 기반으로 정렬하고, 이러한 행위를 가장 큰 자릿수(Most Significant Digit)까지 행한다.
Key Points for radix sort algorithm
- Radix Sort는 선형의 정렬 알고리즘이다.
- Radix Sort의 시간 복잡도는 $O(nd)$로, 배열의 크기는 n이며, d는 가장 큰 수의 자릿수이다.
- 이는 In-place sorting 알고리즘이 아니므로, 추가 공간이 필요하다.
- Radix sort는 Stable Sort로, 상대적인 순서가 보존된다.
- Radix sort는 다른 merge sort나 quick sort보다 느릴 수 있다. 만약 inset(삽입), deletion(삭제), 특정 자릿수의 값 구하기와 같은 operation이 충분히 효율적이지 않은 경우에 말이다.
- Radix Sort는 자릿수나 알파벳 그 자체에 의존하기 때문에 다른 정렬 방법들보다 덜 유연하다.
void countSort(int arr[], int n, int exp) {
int buffer[n];
int i, count[10] = {0};
// exp의 자릿수에 해당하는 count 증가
for (i = 0; i < n; i++){
count[(arr[i] / exp) % 10]++;
}
// 누적합 구하기
for (i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 일반적인 Counting sort 과정
for (i = n - 1; i >= 0; i--) {
buffer[count[(arr[i]/exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
for (i = 0; i < n; i++){
arr[i] = buffer[i];
}
}
void radixsort(int arr[], int n) {
// 최댓값 자리만큼 돌기
int m = getMax(arr, n);
// 최댓값을 나눴을 때, 0이 나오면 모든 숫자가 exp의 아래
for (int exp = 1; m / exp > 0; exp *= 10) {
countSort(arr, n, exp);
}
}
int main() {
int arr[] = {170, 45, 75, 90, 802, 24, 2, 66};
int n = sizeof(arr) / sizeof(arr[0]); // 좋은 습관
radixsort(arr, n);
for (int i = 0; i < n; i++){
cout << arr[i] << " ";
}
return 0;
}
질문
왜 낮은 자릿수(LSD)부터 정렬합니까?
- LSD의 경우 1600000와 1을 비교할 때 Digit의 개수만큼 따져야하는 단점이 있다. 그런데도?
- LSD와 달리 MSD의 경우 비일관된 알고리즘으로 구현이 까다롭다.
참고
- https://www.codingeek.com/algorithms/radix-sort-explanation-pseudocode-and-implementation/
'TIL💡 > Algorithms' 카테고리의 다른 글
| [백준] 17484번: 진우의 달 여행(Small) (0) | 2022.11.26 |
|---|---|
| [백준] 햄버거 분배 (0) | 2022.11.19 |
| [백준] 17779번: 게리맨더링2 (0) | 2022.10.15 |
| [백준] 17140번: 이차원 배열과 연산 (0) | 2022.10.15 |
| [백준] 17143번: 낚시왕 (좌우 반복 이동 구현💡) (0) | 2022.10.14 |