2022. 6. 16. 15:09ㆍTIL💡/AI
앞 장에서 신경망의 가중치 매개변수의 기울기(정확히는 가중치 매개변수에 대한 손실 함수의 기울기)는 수치 미분을 사용해 구했다.
수치 미분은 단순하고 구현하기도 쉽지만 계산 시간이 오래 걸린다는 게 단점이다.
오차역전파법은 가중치 매개변수의 기울기를 효율적으로 계산하도록 한다.
- 순전파(forward propagation): 계산을 왼쪽에서 오른쪽으로 진행
- 역전파(backward propagation): 계산을 오른쪽에서 왼쪽으로 진행
역전파를 통해 미분값을 전달할 수 있고, 각 변수의 미분을 효율적으로 구할 수 있다.

연쇄 법칙(Chain Rule)💡

1학년 미적분학I 시간에 가장 열심히 공부했던 체인룰...
역전파의 계산 절차는 신호 $E$에 노드의 국소적 미분($\frac{\partial y}{\partial x}$)을 곱한 후 다음 노드로 전달하는 것이다. 여기에서 말하는 국소적 미분은 순전파 때의 $y = f(x)$ 계산의 미분을 구한다는 것이며, 이는 $x$에 대한 $y$의 미분($\frac{\partial y}{\partial x}$)을 구한다는 뜻이다. 가령 $y = f(x) = x^2$이라면 $\frac{\partial y}{\partial x} = 2x$가 된다.
그리고 이 국소적인 미분을 상류에서 전달된 값에 곱해 앞쪽 노드로 전달하는 것이다.
연쇄법칙을 설명하려면 우선 합성 함수 이야기부터 시작해야 한다. 합성 함수란 여러 함수로 구성된 함수이다.
예를 들어 $z = (x + y)^2$이라는 식은 아래처럼 두 개의 식으로 구성된다.
$z = t^2$
$t = x + y$
연쇄 법칙은 합성 함수의 미분에 대한 성질이며, 다음과 같이 정의된다.
합성 함수의 미분은 함성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
공식과 증명은 이미 알고 있기 때문에 생략한다.(Latex 쓰기 너무 귀찮다)
역전파는 연쇄법칙의 원리와 동일하다.
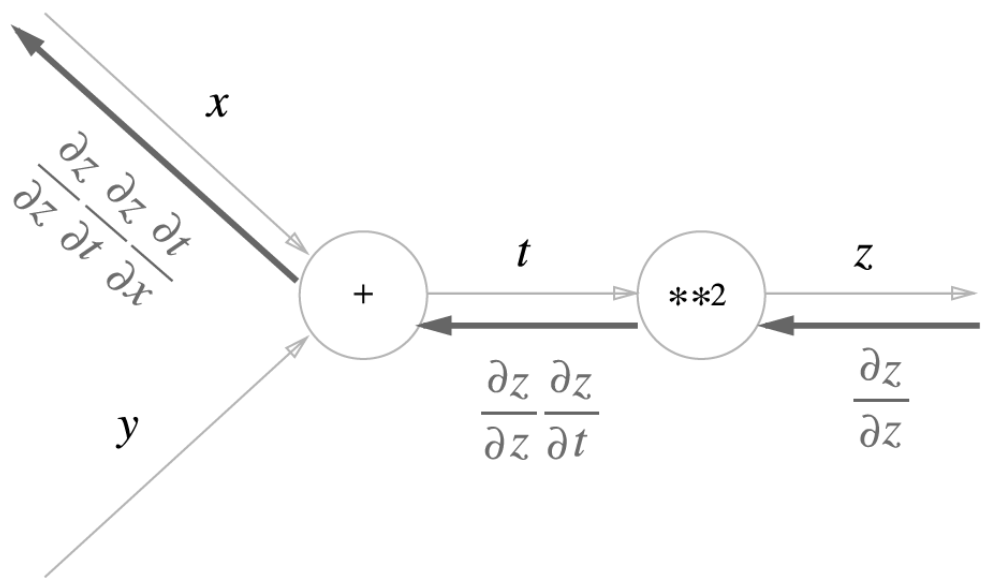
계산 그래프의 역전파는 오른쪽에서 왼쪽으로 신호를 전파한다. 역전파의 계산 절차에서는 노드로 들어온 입력 신호에 그 노드의 국소적 미분(편미분)을 곱한 후 다음 노드로 전달한다.
맨 왼쪽 역전파를 보면 연쇄법칙처럼 $\frac{\partial z}{\partial z}\frac{\partial z}{\partial t}\frac{\partial t}{\partial x} = \frac{\partial z}{\partial x}$이 성립되어 x에 대한 z의 미분이 된다.
Affine / Softmax 계층 구현하기
Affine 계층
신경망의 순전파에서는 가중치 신호의 총합을 계산하기 때문에 행렬의 곱(넘파이에서는 np.dot())을 사용했다.
행렬의 곱 계산은 대응하는 차원의 원소 수를 일치시키는 게 핵심이다.
신경망의 순전파 때 수행하는 행렬의 곱은 기하학에서는 어파인 변환(Affine Transformation)이라고 한다. 그래서 이 책에서는 어파인 변환을 수행하는 처리를 Affine 계층이라는 이름으로 구현한다.
Softmax-with-Loss 계층
마지막으로 출력층에서 사용하는 소프트맥스 함수에 관해 설명해보자. 앞에서 말했듯이 소프트맥스 함수는 입력 값을 정규화하여 출력한다.

신경망에서 수행하는 작업은 학습과 추론 두 가지이다. 추론할 때는 일반적으로 Softmax 계층을 사용하지 않는다. 예컨대 신경망은 추론할 때는 마지막 Affine 계층의 출력을 인식 결과로 이용한다.
또한 신경망에서 정규화하지 않은 출력 결과(Softmax 앞의 Affine 계층의 출력)를 점수(score)라 한다.
즉, 신경망 추론에서 답을 하나만 내는 경우에는 가장 높은 점수만 알면 되니 Softmax 계층은 필요 없다는 것이다.
반면, 신경망을 학습할 때는 Softmax 계층이 필요하다.

여기서 exp, log 노드를 거치면 왜 이런 연산 결과가 나올까? 미분을 쓰는 거 같은데..
궁금해서 책 후반의 Appendix를 찾아보았다.
크게 두 파트로 나누어 역전파를 계산한다.
Cross Entrophy Error 계층의 역전파
- 역전파의 초깃값, 즉 가장 오른쪽의 역전파의 값은 1이다.($\frac{\partial L}{\partial L} = 1$이므로)
- 'x' 노드의 역전파는 순전파 시의 입력들의 값을 서로 바꿔 상류의 미분에 곱하고 하류로 흘린다.
- '+' 노드의 역전파는 상류에서 전해지는 미분을 그대로 흘린다.
- 'log' 노드의 역전파는 다음 식을 따른다. ✨
$y = log x$
$\frac{\partial y}{\partial x} = \frac{1}{x}$
Softmax 계층의 역전파
1단계
앞 계층(Cross Entropy Error 계층)의 역전파 값이 흘러온다.
2단계
'x' 노드에서는 순전파의 입력들을 '서로 바꿔' 곱한다.
$y_1 = \frac{exp(a_1)}{S}$
$\frac{t_1}{y_1}exp(a_1) = - t_1 \frac{S}{exp(a_1)} exp(a_1) = - t_1S$
3단계
순전파 때 여러 갈래로 나뉘어 흘렸다면 역전파 때는 그 반대로 흘러온 여러 값을 더한다. 그래서 여기에서는 3개의 갈라진 역전파의 값을 모두 더한다. 이 더해진 값이 '/' 노드의 역전파를 거쳐 $\frac{1}{S}(t_1 + t_2 + t_3)$이 된다.
'/'노드의 역전파는 '상류에서 흘러온 값'에 '순전파 때의 출력을 제홉한 후 마이너스를 붙인 값'을 곱해 하류로 전달한다.
'/' 노드는 단순 나눗셈이 아니라 역수의 효과를 띄기 때문이다.
$y = \frac{1}{x} = x^{-1}$
$\frac{\partial y}{\partial x} = -\frac{1}{x^2}$
여기에서 '상류에서 흘러온 값'은 $(-t_1S) + (-t_2S) + (-t_3S) = -S(t_1 + t_2 + t_3)$이고, '순전파 때의 출력'은 $\frac{1}{S}$이므로 $-S(t_1 + t_2 + t_3) * -\frac{1}{S^2} = \frac{1}{S}(t_1 + t_2 + t_3)$가 된다.
그런데 여기에서 $(t_1, t_2, t_3)은 원-핫 벡터로 표현된 정답 레이블이다. 원-핫 벡터란 (t_1, t_2, t_3) 중 단 하나만 1이고 전부 0임을 뜻한다. 따라서 합은 1이 된다.$
4단계
'+' 노드는 입력을 여과없이 내보낼 뿐이다.
5단계
여러 번 나왔듯이 'x' 노드는 입력을 '서로 바꾼' 곱셈이다. 여기에서는 $y_1 = \frac{exp(a_1)}{S}$를 이용해 식을 변형했다.
6단계
쟁점: output이 2개 이상인 경우에는?
'exp' 노드에서는 다음 관계식이 성립된다.
$y = exp(x)$
$\frac{\partial y}{\partial x}=exp(x)$
그리고 두 갈래의 입력의 합에 $exp(a_1)$을 곱한 수치가 여기에서 구하는 역전파이다.
output이 2개 이상($\frac{1}{S}, -\frac{t_1}{exp(a_1)}$)이므로 두 output을 더하고, $exp(a_1)$을 곱해준다.
이를 변형하면 $y_1 - t_1$이 된다. 이상에서 순전파의 입력이 $a_1$인 첫 번째 노드에서는 역전파가 $y_1 - t_1$임이 유도되었다. 나머지의 역전파에도 같은 순서로 구할 수 있다.
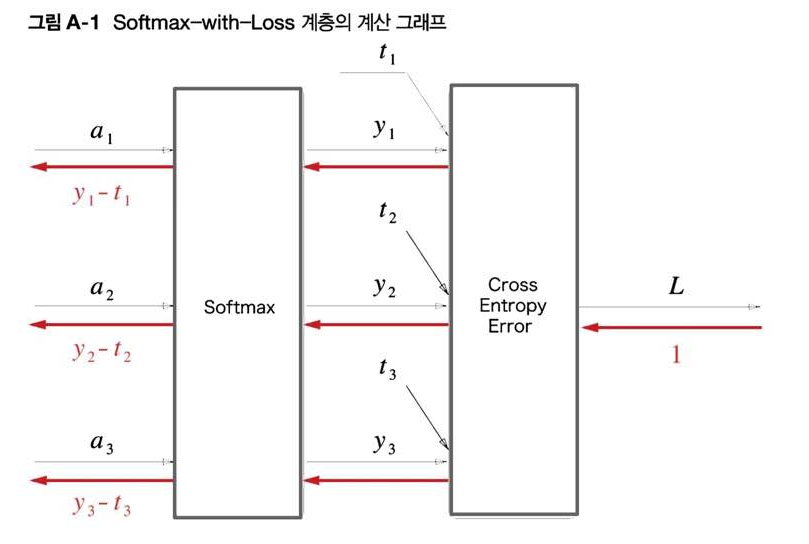
Softmax 계층은 입력 $(a_1, a_2, a_3)$를 정규화하여 $(y_1, y_2, y_3)$를 출력한다. Cross Entropy Error 계층은 Softmax의 출력 $(y_1, y_2, y_3)$와 정답 레이블 $(t_1, t_2, t_3)$를 받고, 이 데이터로부터 손실 $L$을 출력한다.
주목할 것은 역전파의 결과이다. Softmax의 역전파는 $(y_1 - t_1, y_2 - t_2, y_3 - t_3)$라는 '말끔한' 결과를 내놓고 있다. 이는 Softmax 계층의 출력과 정답 레이블의 차분인 것이다. 신경망의 역전파에서는 이 차이인 오차가 앞 계층에 전해지는 것이다. 이는 신경망 학습의 중요한 성질이다.
그런데 신경망 학습의 목적은 신경망의 출력이 정답 레이블과 가까워지도록 가중치 매개변수의 값을 조정하는 것이었다. 그래서 신경망의 출력과 정답 레이블의 오차를 효율적으로 앞 계층에 전달해야 한다. 앞의 $(y_1 - t_1, y_2 - t_2, y_3 - t_3)$라는 결과는 바로 Softmax 계층의 출력과 정답 레이블의 차이로, 신경망의 현재 출력과 정답 레이블의 오차를 있는 그대로 드러내는 것이다.
오차 역전파법으로 구한 기울기 검증하기
수치미분은 느리지만, 오차역전파법으로 구한 기울기를 정확히 구현했는지 확인하기 위해 필요하다.
수치 미분과 오차역전파법의 결과 오차가 0이 되는 일은 드물다. 이는 컴퓨터가 할 수 있는 계산의 정밀도가 유한하기 때문이다.
(가령 32비트 부동소수점)
이 정밀도의 한계 때문에 오차는 대부분 0이 되지는 않지만 올바르게 구현했다면 0에 아주 가까운 작은 값이 된다. 만약 그 값이 크면 오차 역전파법을 잘못 구현했다고 의심해봐야 한다.
정리
- 계산 그래프를 이용하면 계산 과정을 시각적으로 파악할 수 있다.
- 계산 그래프의 노드는 국소적 계산으로 구성된다. 국소적 계산을 조합해 전체 계산을 구성한다.
- 계산 그래프의 순전파는 통상의 계산을 수행한다. 한편, 계산 그래프의 역전파로는 각 노드의 미분을 구할 수 있다.
- 신경망의 구성 요소를 계층으로 구현하여 기울기를 효율적으로 계산할 수 있다.(오차역전파법).
- 수치 미분과 오차역전파법의 결과를 비교하면 오차역전파법의 구현에 잘못이 없는지 확인할 수 있다기울기 확인).
'TIL💡 > AI' 카테고리의 다른 글
| [논문] BERT: Attention Is All You Need 읽기 (0) | 2022.07.31 |
|---|---|
| AI RUSH 2022 참가 🏃♀️ (0) | 2022.06.18 |
| 4장. 신경망 학습 (0) | 2022.06.12 |
| 3장. 활성화 함수(Step Function) (0) | 2022.06.08 |
| 딥러닝 추천 강의 기록 (0) | 2022.06.05 |