2022. 5. 23. 14:12ㆍTIL💡/Algorithms
💚1933 스카이라인
N개의 직사각형 건물이 있을 때 스카이라인을 구하는 문제
스카이라인을 차례대로 left x, h, right x 우선순위에 대한 오름차순으로 정렬한다.
이래야만 추후 점들을 대체하는 작업이 순조롭게 이루어진다.
이 문제의 핵심은 두 개의 스카이라인이 교차할 때 높이를 어떻게 결정할 것인가이다. 정답은 교차 시 더 높은 h값을 선택해야 한다.(max 사용)
그리고 추가적으로 동일한 x일 때, 동일한 h일 때에 대한 경우도 고려해야 한다.
가장 어려웠던 점이 대체 후에 동일한 경우까지 따져야한다는 점이 어려웠다.
#include <iostream>
#include <vector>
#include <tuple>
#include <algorithm>
using namespace std;
using Result = vector<pair<int,int>>;
struct Building {
int left, right, height;
};
// first : x, second : h
void append(Result &ans, pair<int, int> p) {
int n = ans.size();
if(n > 0) {
// h값이 동일한 경우 추가 X
if(ans[n - 1].second == p.second) {
return;
}
// x값이 동일한 경우 더 h값이 큰 걸로 대체
if(ans[n - 1].first == p.first) {
ans[n - 1].second = p.second;
// 만약 교체 후 그보다 이전의 h값과 동일하다면 스카이라인 변경이 없으므로 제거
if(n > 1 && ans[n - 2].second == ans[n - 1].second) {
ans.pop_back();
}
return;
}
}
ans.push_back(p);
}
Result merge(Result &l, Result &r) {
Result ans;
// 왼쪽 스카이라인의 현재 높이
int h1 = 0;
// 오른쪽 스카이라인의 현재 높이
int h2 = 0;
int i = 0;
int j = 0;
while(i < l.size() && j < r.size()) {
auto &u = l[i];
auto &v = r[j];
// 등호 처리 중요
// 만약 u.first == v.first면, 정렬 우선순위상 v보다 u의 height가 작거나 right가 작다는 의미가 내포
// 따라서 u가 먼저 append되는 것이 맞다.
if(u.first <= v.first) {
int x = u.first;
h1 = u.second;
int h = max(h1, h2);
append(ans, make_pair(x, h));
i++;
}
else {
int x = v.first;
h2 = v.second;
// 더 큰 높이로 선택
// 만약 높이가 동일한 점이 있다면
int h = max(h1, h2);
append(ans, make_pair(x,h));
j++;
}
}
while(i < l.size()) {
int x = l[i].first;
h1 = l[i].second;
int h = max(h1, h2);
append(ans, make_pair(x, h));
i++;
}
while(j < r.size()) {
int x = r[j].first;
h2 = r[j].second;
int h = max(h1, h2);
append(ans, make_pair(x, h));
j++;
}
return ans;
}
Result go(vector<Building> &a, int start, int end) {
if(start == end) {
Result ans = {
{a[start].left, a[start].height},
{a[start].right, 0}
};
return ans;
}
int mid = (start + end) / 2;
// left and right
auto l = go(a, start, mid);
auto r = go(a, mid + 1, end);
return merge(l, r);
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<Building> a(n);
for(int i = 0;i < n;i++) {
cin >> a[i].left >> a[i].height >> a[i].right;
}
// left, height, right 순으로 오름차순 정렬
sort(a.begin(), a.end(), [](Building &u, Building &v) {
return make_tuple(u.left, u.height, u.right) < make_tuple(v.left, v.height, v.right);
});
auto ans = go(a, 0, n - 1);
for(auto &p : ans) {
cout << p.first << ' ' << p.second << ' ';
}
cout << '\n';
return 0;
}💚2261 가장 가까운 두 점
2차원 평면 위의 N개의 점 중에서 가장 가까운 두 점을 찾는 문제
2 <= N <= 100,000
모든 점의 쌍을 조사하면 O(N^2)이 걸린다. -> 시간 초과
먼저 점을 X 좌표가 증가하는 순으로 정렬
중간에 있는 점을 찾는다.
중간에 있는 점을 기준으로 왼쪽과 오른쪽으로 나눈다.
- 왼쪽: PL
- 오른쪽: PR
- PL에서 가장 가까운 두점 dL(왼쪽에서의 최솟값)
- PR에서 가장 가까운 두점 dR(오른쪽에서의 최솟값)
d = min(dL, dR)이라고 했을 때
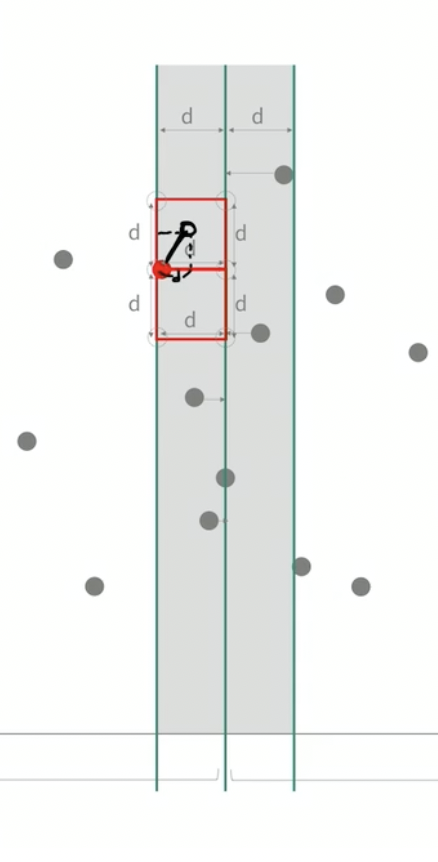
가운데 점으로부터 -d, +d만큼 떨어진 곳에서 가장 가까운 두 점을 찾아야 한다.
만약 -d, +d 구간에 지나치게 점이 많으면 비효율적이다.
그런데 예를 들어 어떤 점의 좌표가 (x,y)였다면 거리를 조사해야하는 y좌표 범위는 [y-d, y+d]이다.
d가 최솟값이라는 전제 하에 이 범위에 들어있는 점의 개수는 최대 6개이다.
각각의 단계마다 회색 영역에 있는 점을 y좌표 순으로 정렬해야 한다. 이렇게 하면 전체 시간 복잡도 O(N(logN)^2)
하지만 만약 미리 점을 y순으로 정렬해놓고 상대적인 순서를 유지한 채로 나눈면 매번 정렬을 하지 않아도 된다.
이렇게 된다면 전체 시간 복잡도 O(NlogN)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct Point {
int x, y;
};
int dist(Point p1, Point p2) {
return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);
}
bool cmp_x(const Point &u, const Point &v) {
return make_pair(u.x, u.y) < make_pair(v.x, v.y);
}
bool cmp_y(const Point&u, const Point &v) {
return make_pair(u.y, u.x) < make_pair(v.y, v.x);
}
int brute_force(vector<Point> &a, int start, int end) {
int ans = -1;
for(int i = start;i < end;i++) {
for(int j = i + 1;j <= end;j++) {
int d = dist(a[i], a[j]);
if(ans == -1 || ans > d) {
ans = d;
}
}
}
return ans;
}
int closest(vector<Point> &a, int start, int end) {
int n = end - start + 1;
if(n <= 3) {
return brute_force(a, start, end);
}
int mid = (start + end) / 2;
int left = closest(a, start , mid);
int right = closest(a, mid + 1, end);
int ans = min(left, right);
// 회색 영역
vector<Point> b;
// x값을 기준으로 회색 영역 정하기
for(int i = start;i <= end;i++) {
int d = a[i].x - a[mid].x;
if(d * d < ans) {
b.push_back(a[i]);
}
}
// 회색 영역 내의 점들 중 y값을 기준으로 왼쪽, 오른쪽에서 구한 최소의 거리보다 작은 거리 구하기
sort(b.begin(), b.end(), cmp_y);
int m = b.size();
for(int i = 0;i < m - 1;i++) {
for(int j = i + 1;j < m;j++) {
int y = b[j].y - b[i].y;
if(y * y < ans) {
int d = dist(b[i], b[j]);
if(d < ans) {
ans = d;
}
}
else {
break;
}
}
}
return ans;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<Point> a(n);
for(int i = 0;i < n;i++) {
int x, y;
cin >> x >> y;
a[i] = {x, y};
}
sort(a.begin(), a.end(), cmp_x);
cout << closest(a, 0, n - 1) << '\n';
return 0;
}x로 정렬했다가, y로 정렬했다가 왔다갔다하면 비효율적이다.
그래서 x와 y로 정렬한 배열 따로 둔다.
x는 분할 정복으로 회색영역을 정할 때, y는 회색 영역 내에서 최단 거리를 구하는 용도로 쓴다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct Point {
int x, y;
};
int dist(Point p1, Point p2) {
return (p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y);
}
bool cmp_x(const Point &u, const Point &v) {
return make_pair(u.x, u.y) < make_pair(v.x, v.y);
}
bool cmp_xe(const Point &u, const Point &v) {
return make_pair(u.x, u.y) <= make_pair(v.x, v.y);
}
bool cmp_y(const Point&u, const Point &v) {
return make_pair(u.y, u.x) < make_pair(v.y, v.x);
}
int brute_force(vector<Point> &a, int start, int end) {
int ans = -1;
for(int i = start;i < end;i++) {
for(int j = i + 1;j <= end;j++) {
int d = dist(a[i], a[j]);
if(ans == -1 || ans > d) {
ans = d;
}
}
}
return ans;
}
int closest(vector<Point> &ax, vector<Point> &ay, int start, int end) {
int n = end - start + 1;
if(n <= 3) {
return brute_force(ax, start, end);
}
int mid = (start + end) / 2;
Point mid_p = ax[mid];
vector<Point> ayl, ayr;
for(Point p : ay) {
if(cmp_xe(p, mid_p)) {
ayl.push_back(p);
}
else {
ayr.push_back(p);
}
}
int left = closest(ax, ayl, start , mid);
int right = closest(ax, ayr, mid + 1, end);
int ans = min(left, right);
// 회색 영역
vector<Point> b;
// x값을 기준으로 회색 영역 정하기
for(Point p : ay) {
int d = p.x - mid_p.x;
if(d * d < ans) {
b.push_back(p);
}
}
int m = b.size();
for(int i = 0;i < m - 1;i++) {
for(int j = i + 1;j < m;j++) {
int y = b[j].y - b[i].y;
if(y * y < ans) {
int d = dist(b[i], b[j]);
if(d < ans) {
ans = d;
}
}
else {
break;
}
}
}
return ans;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<Point> ax(n);
vector<Point> ay(n);
for(int i = 0;i < n;i++) {
int x, y;
cin >> x >> y;
ax[i] = {x, y};
ay[i] = {x, y};
}
sort(ax.begin(), ax.end(), cmp_x);
sort(ay.begin(), ay.end(), cmp_y);
cout << closest(ax, ay, 0, n - 1) << '\n';
return 0;
}'TIL💡 > Algorithms' 카테고리의 다른 글
| [네트워크] STP (0) | 2022.05.23 |
|---|---|
| [중급 알고리즘] 이분 탐색 (0) | 2022.05.23 |
| [중급 알고리즘] 분할 정복(연습) (0) | 2022.05.18 |
| [중급 알고리즘] 그리디(도전) (0) | 2022.05.17 |
| [중급 알고리즘] 그리디 (연습) (0) | 2022.05.16 |